最近開源社區裡的基於ChatGPT的問答和LLAMA模型微調的羊駝系列非常火爆。而筆者所看到的大部分低成本復現ChatGPT項目《除了ClossalAI》都隻包含了基於人類偏好回復的SFT階段,而不包括後面的RLHF階段。 同時網上有幾個開源的使用PPO《或類PPO算法》來更新語言模型的代碼庫,他們的實現略有不同,有將問答建模成基於詞級別的馬爾科夫決策過程的,也有基於句子級別的建模成bandit problem的方式。也有添加了不同約束項的各種實現。如何看明白他們的涵義和挑選出適合當前任務/實驗所需的部分加以改進,是個現實的問題。
所以這篇筆記將會記載筆者為了入門RLHF看懂他們的公式設計意圖的歷程,並整理筆者最近一段時間在學習跟ChatGPT相關的PPO知識時讀過的一些直接相關的技術博客,論文等資料,做簡單的點評以供未來筆者回憶時查詢。
包含了RLHF實現的一些開源框架
以下是筆者梳理的強化學習裡策略梯度到RLHF的PPO相關的一些內容,對強化學習已有相當了解的可以跳過到最後一部分筆者訓練RLHF的內容。
1:強化學習基礎概念復習
筆者除了在碩士時了解過value-based RL之後三四年沒碰過強化學習了,Lilian-Weng的技術博客非常全面,細致地梳理了RL的基本概念,value-based到policy-based的發展脈絡。非常適合有類似需要的復習一遍。其中value-based 的方法裡重點復習一下td-lambda的思想和推導過程,不僅非常核心且推導過程會在下面的Generalized Advantage Estimation(GAE)裡再見到。
Lilian-Weng: A (Long) Peek into Reinforcement Learning : https://lilianweng.github.io/posts/2018-02-19-rl-overview/#monte-carlo-methods
2: 策略梯度基礎入門
筆者閱讀上一部份lilian-weng的 Long Peek into RL裡的policy gradients章節時覺得不夠清楚。於是在這個部分推薦讀一位 UCB的博士《現CMU博士後的robotics大佬》Daniel Seita在17年整理的策略梯度推導。即詳盡,又清晰,讀起來神清氣爽,讀完後對策略梯度推導過程,其訓練時會有哪些問題《如多步采樣引起的方差過大不穩定》,如何解決《引入baseline》,為什麼這樣解決(為什麼這樣引入baseline既無偏又能降低方差),有個比較宏觀的了解。
Going Deeper Into Reinforcement Learning: Fundamentals of Policy Gradients: https://danieltakeshi.github.io/2017/03/28/going-deeper-into-reinforcement-learning-fundamentals-of-policy-gradients/
3. GAE論文
GAE Paper: HIGH-DIMENSIONAL CONTINUOUS CONTROL USING GENERALIZED ADVAN他GE ESTIMATION
在讀Daniel Seita的策略梯度推導時,其實已經包括了GAE將要涵蓋的一些概念,即如果baseline是advantage function我們可以獲得一個最低方差的無偏估計。可如何有效地預估和近似這個優勢方程,則需要構建一個近似的有偏優勢方程(gamma-just-estimator)。以下是筆者總結的GAE幾點摘要速覽:
1: 策略梯度的朴素估計方差過大,難以收斂。通過引入baseline function可以很好地減弱這個問題的影響。其中如果baseline function是優勢方程advantage function時理論上可以得到最低方差。《即每次策略梯度更新的方向必然是增大那些比當前狀態的『平均』動作更優的動作,降低比平均動作更劣的動作》
2:注意在策略梯度的推導裡《GAE論文和上面Daniel Seita的推導》,我們並沒有引入衰減因子discount factor。這樣得到的使用優勢方程作為基線方程的策略梯度估計雖然無偏且方差小,但是優勢方程不好預估。我們轉而引入衰減因子,來預估一個無偏的優勢方程 A^{\pi,\gamma} 。這將使我們得到無偏的帶衰減因子的有偏策略梯度 g^{\gamma} 。但注意我們的目標是預估一個沒有引入衰減因子的無偏策略梯度g,但引入了衰減因子的策略梯度 g^{\gamma } 其本身是有偏的《哪怕對其的預估是無偏的》,所以GAE是一個對無偏策略梯度g使用了有偏策略梯度 g^{\gamma} 的近似。
3:關於gamma-just-estimator的證明可以看Daniel-seita 對這篇論文的點評筆記notes on GAE paper: https://danieltakeshi.github.io/2017/04/02/notes-on-the-generalized-advantage-estimation-paper/
4: 因為GAE論文裡的公式《10》,為了得到優勢方程的預估,我們需要預估值方程V(st)。且該值方程需滿足定義 V = V^{\pi,\gamma}(s_t) = \mathbb{E}_{s_{t+1:\infty,a_t:\infty}} [\Sigma_{l=0}^{\infty}\gamma^lr_{t+l}] 。當且僅當他們相等時,該預估是gamma-just,且我們得到衰減優勢方程 A^{\pi,\gamma} 的無偏估計。注意這裡對定義在無限步長上的值方程的加權配比以及求和用到了TD-lambda一模一樣的推理過程,隻是這次是用來預估優勢方程而不是值方程。

5:lambda和gamma都是衰減系數,隻是涵義不同。我們知道lambda=0在TD-lambda裡代表的是Q-learning的一步近似,而Lambda=1是等價於MC的無偏估計。所以lambda值的調整在GAE的語境下是類似的調整bias-variance的一個權衡值。gamma的情況非常類似,gamma是我們選取的獎勵值的一個衰減因子,它的引入不僅影響值方程的尺度大小同時也帶來了偏差。但作者提到當gamma<1時,無論值方程的準確度如何都會帶來偏差《值方程的準確度實際上也受gamma的很大影響,因為其決定了值方程所涵蓋的步數》,而lambda<1時僅當值方程不準確時會帶來偏差。這是由他們的作用與涵義所決定的,同時作者提到他們實驗裡lambda的最佳值一般顯著低於gamma值。至此我們所希望估計的有偏策略梯度就變成了:

6:Reward shaping 隻是以另外一種角度看待上面推出的GAE。因為將獎勵重新映射後上面所推的所有公式不變,唯一改變的隻是lambda和gamma被統一到一個參數上。
7:作者使用了TRPO的思想來更新策略梯度,但同時也使用了Trust Region的思想來更新值方程。作者認為這樣能夠更好地防止值方程過度擬合最近批次的數據。
GAE的主要貢獻在於提出了一個使用gamma,lambda來權衡偏差和方差的泛化優勢預測器GAE,並且使用trust region的算法來優化策略和值方程,最終使得一些更復雜《狀態空間和動作空間維度更廣》的問題求解成為可能。
4:Natural Policy Gradient + TRPO + PPO
前面幾節的內容都在討論策略梯度的整體更新公式,但具體到如何策略更新時我們會面臨很多問題,比如采樣效率的問題,比如選擇步長的問題(這兩個實際是關聯問題)。步長的選擇之所以是問題是因為參數更新的距離並不等價於我們的策略分佈更新的距離。試考慮以下兩組高斯分佈間的參數距離和分佈距離,他們的參數差《均值和方差的均方誤差MSE》相等,但明顯他們的分佈差極大。而強化學習相比於常見的有監督學習更不穩定,其中一部分原因便是因為策略的更新所導致的觀測狀態,獎勵的分佈變化。無法很好地決定訓練步長的一個副作用就是樣本利用率不高,收斂慢或難以收斂。而natural policy gradient ,TRPO 和PPO則是試圖解決這個 問題的幾種思路。

I:Natural Policy Gradient
其中要看懂natural policy gradient需要幾項一些優化理論的前置知識《包括常見的拉格朗日松弛法,Fisher-info-Matrix以及它和KL散度,Hessian矩陣的關聯等》,如果有不熟悉的讀者可以先查閱這幾個基礎概念的定義,再看natural policy gradient就水到渠成了《btw 擴散模型裡score matching相關的內容涉及了大量這方面的優化概念》。
具體來說因為在參數空間上的歐式距離不等價於我們所希望的策略分佈上的距離,我們轉而使用KL散度來約束我們每次梯度更新的大小。這個約束可以用拉格朗日松弛法來將約束轉化為懲罰項。

對這個懲罰項裡的KL散度求解可以用泰勒展開來近似(因為我們不知道策略分佈的具體形式,如果遍歷狀態和動作空間來求解過於復雜)。其中會用到KL散度的泰勒二階展開在theta值附近等於Fisher Matrix的性質。而求二階導我們也不用特地求解Hessian矩陣《計算復雜度在O(KN^2)左右,其中K為單個元素計算復雜度》,而是可以利用score即 log\pi_{\theta}(x) 的梯度來求得,計算復雜度大大下降。最終,我們的計算會變成以下結果:梯度的形式由原先的損失梯度變為使用費舍矩陣的逆乘上原梯度(使得梯度考慮到KL散度的分佈限制),再乘上我們的動態步長《約束我們的更新必須小於設定的 \epsilon 》。
其中以KL散度約束梯度下降並使用FIM求解的方法就叫做自然梯度法,natural gradients method 也是該論文名稱的由來。
參考資料
FIM和KL散度的關系: Transfer G:Fisher Information matrix(FIM)的性質,與Hessian,KL divergence的關聯
自然梯度解析:https://towardsdatascience.com/natural-policy-gradients-in-reinforcement-learning-explained-2265864cf43c
II:TRPO
自然策略梯度聽起來很美好,但實際上使用有非常多的問題。其中幾個問題在於對費舍矩陣(theta的outer product)求逆的計算量,以及該算法其本身的不穩定《采樣來近似期望,泰勒展開的近似,局域臨近性的假設等》。這些問題導致了策略梯度方法往往在很多問題上效果不佳或者不收斂。而TRPO對這幾個問題提出了針對性的改進,使得其能夠在大量參數下《以往的方法需要求解計算復雜度極高的Hessian 矩陣》且相對復雜的場景下取得優秀的效果。
關於TRPO的講解知乎已經有非常詳盡的分享了,筆者在此不再贅言。附上鏈接:天津包子餡兒:強化學習進階 第七講 TRPO 。
在此筆者記錄幾個筆者認為關鍵的要點:
1:自然梯度法所求解的策略梯度更新方法有著極多的限制,為了折中計算的復雜度使得計算更加可行,TRPO進行了多次近似。
2:其中原文中非常關鍵的一個式子如下。注意兩點。其一是新舊策略的差別是定義在所有的狀態和動作空間上的優勢函數求和(參考Kakade的CPI Conservative Policy Iteration,隻是CPI裡的優勢函數是定義在時間步上求和,而TRPO是定義在狀態空間上求和)。即如果可以保證下面式3的右側優勢函數每輪更新都單調遞增的話,我們就保證了策略更新所帶來的期望獎勵單調遞增。其二 是對新策略的期望獎勵 \eta(\widetilde{\pi}) 的近似 L_{\pi}(\widetilde{\pi}) 是通過舊策略來得到的。其依據是如果新舊策略差別不明顯時,可以用舊策略對所有狀態的的訪問頻率來近似估計新策略的期望折扣獎勵。這樣的近似避免了要計算所有可能的新策略對所有狀態所對應的訪問頻率,所帶來的優化難題。

3:TRPO是一種minorization-maximization(MM)算法,作者通過拓展了conservative-policy-iteration裡提出的下界的形式,實現策略的目標在迭代中隻增不減。其中CPI的優化下界如下圖公式6所顯示。TRPO通過將alpha替換為Total_Variance的距離測度後,推導證明了新的下界來取代CPI的下界,其中因為total varaicne的測度距離一定小於等於KL測度距離,最終得到了式9。


4:以上的理論部分證明的是如果我們按照以下的式子優化,則可以保證我們每步更新的策略的單調提升《即期望獎勵值 \eta 的提升》。

但是如果按照上述所推導的策略更新方式收斂過慢,步幅太小。於是還是回到自然梯度法裡的引入硬約束trust region \delta 。於是得到式11。
但式11要求基於每個狀態的策略分佈的最大KL距離小於硬約束,實際太難求解於是轉而近似要求所有狀態上的策略分佈距離的KL距離均值小於約束值得到式12。
將式12裡的損失函數展開成其定義,即上述式3裡提到的最大化每個狀態裡的優勢函數值的提升,得到式13。
將式13裡的優勢函數轉化為Q,不影響其單調性。同時將新策略的動作空間上的求和轉換為重要性采樣的預估值後我們得到式14。也就是我們的最終優化目標。

5: 但是需要注意的是TRPO的理論更新方式和實際實現的更新方式有較大差異《論文第六章》:如果我們嚴格按照TRPO的公式推導來更新每步的梯度,則更新幅度會特別小收斂速度特別慢(因為懲罰項C過大)。所以TRPO的實際更新方式《采用基於硬約束項 \delta 》如下:1. 使用了共軛梯度法《Conjugate Gradients)來近似求解硬約束項的更新步幅,取代了自然梯度法裡用費舍矩陣的逆求解的方法。2.用線性搜索《Line Search》的方法,來檢驗共軛梯度法求解的更新步幅是否符合硬約束項的要求。如果不符合,則指數縮小步幅直到符合約束《自然梯度法本身並不檢查這一項,且由於泰勒展開的近似性,局域臨近性的要求等,硬約束本身常被違背》。3. 除了檢驗更新前後的策略分佈的KL散度的距離外,該算法還實際檢測了更新後我們的代理損失函數(surrogate loss)式14,是否確實提升。
理解TRPO的最終做法對理解PPO的實現方式為何簡單有效十分重要,值得仔細閱讀論文。
III:PPO
前面提到TRPO雖然用了詳細的推導論證了基於懲罰項的理論更新值可以保證策略回報單調提升《即TRPO式9》,但實際實現時依然使用了類似自然梯度法的基於硬約束的方式來決定梯度更新的步長。隻是在計算硬約束的情況下,TRPO使用了共軛梯度法,線性搜索和策略檢驗等方法來檢測更新效果。PPO的實現也分兩種,第一種是在式9的基礎上動態調整KL約束項的懲罰系數C,來達到約束參數更新的幅度的目的。即參數的更新應盡可能的小以保證訓練的穩定,但同時應在分佈空間更新得足夠的大以使得策略分佈發生改變。如下圖的算法所示,對於更新前後的KL距離,我們設定一個目標約束值 \delta 《一個可調整的超參》。如果當前的更新大於1.5倍目標約束值《1.5是個經驗設定值,並非推導所得》則策略分佈波動過大,我們增大懲罰系數《乘2》,若KL距離小於目標約束值的2/3,則策略分佈更新過小,我們減小懲罰系數《除以2》。雖然PPO的這種更新方式並沒有嚴格的數學推導,並且時不時地更新幅度會過大或過小,違背了策略單調提升的要求。但從實際部署的效果來看,PPO往往能夠快速調整懲罰系數的權重,來快速適應訓練的不同階段的要求,並且效果良好。
第二種方法同樣對應TRPO裡使用trust region 直接設置KL散度的最大更新約束值。但是和使用KL散度的約束值不同的是該方法是對優勢函數做了限制。其中當重要性采樣的系數 r_t(\theta) 大於或小於 1 \pm \epsilon 時,該更新會被忽略《根據 \epsilon 裁剪後的損失不依賴於參數所以不產生任何梯度信息》。本質上是忽略了差異過大的新策略所產生的優勢函數值,保證了訓練的穩定性和梯度更新的單調遞增所需的步幅小的要求。注意因為優勢函數的值可以取正負,且重要性系數是新策略的可能性除以舊策略的可能性,為了最大化優勢函數的期望值我們希望當優勢函數A>0時,系數大於一《但不能過大》,優勢函數A<0時,系數小於一《但不能過小》。理論上因為采用min函數來選取優化目標當A>0時,系數的argmax值取小於 1-\epsilon 的時候,以及A<0時,系數的argmax值取大於 1+\epsilon 的時候均不受裁剪的影響。但這種情況是否會發生,多經常發生,是否影響訓練效果筆者尚不清楚。
具體推導可以參考原論文和或以下兩篇技術博客
5:策略梯度發展歷程梳理
在閱讀完以上幾篇策略梯度的技術博客後,再回過頭來看lilian-weng在intro to RL之後的policy gradients 脈絡梳理就比較容易抓住重點了。其中注意目前開源的大部分RLHF的實現都基於On Policy的Actor Critic算法。
Lilian-Weng Policy Gradient Algorithms: https://lilianweng.github.io/posts/2018-04-08-policy-gradient/
6:InstructGPT & RL4LM
InstructGPT: Training language models to follow instructions with human feedback
關於這篇經典的RLHF論文,筆者在這裡隻討論裡面的RLHF公式以及相對應的一些代碼庫是如何實現的。首先在instructGPT裡,我們將期望優化的語言模型用策略 \pi^{RL}_{\phi} 來表示《該語言模型的參數將在RLHF階段更新》,而經過SFT的語言模型用 \pi^{SFT} 來表示《該語言模型不參與RLHF階段的更新》,同時反饋模型RM用 r_{\theta}(x,y) 表示。這個公式的涵義是我們希望最大化反饋模型的獎勵值,但同時希望我們RLHF階段的語言模型的輸出分佈,不要距離SFT指令微調後的分佈太遠《即雖然InstructGPT裡將語言模型的回答建模成了bandit problem,但第二項KL散度的約束是基於詞粒度的,防止語言模型過度針對獎勵值優化》。除此之外,模型還需要做一些預訓練任務《下式第三項》以保證其預訓練的能力不會過分退化。
注意式2長得很像TRPO裡的優化公式9,筆者曾疑惑為何約束更新的策略不是上一步的策略而是一個靜態的SFT策略模型。這樣是否依然能夠滿足策略梯度模型性能單調增強的KL臨近性需求。但仔細回想上文裡TRPO到PPO的演化進程就可以想明白,公式2裡的KL散度約束,的確如原文所說,隻是為了防止所優化的語言模型過度傾向於獎勵模型。而真正策略梯度更新所要求的策略分佈的變化值小於約束值是體現在了公式之外的PPO-clipping算法裡。值得一提的是,在下面的RL4LM的消融實驗裡提出了一個很有意思也很符合直覺的觀點,即如果SFT模型本身仍不具備RLHF所希望其習得的能力或能力較差,那麼SFT的約束反而會有反效果。
注意看以下clossal AI裡的RLHF-PPO實現 ,裡面Policy的損失很明顯就是按照PPO的方式一字不差地實現。
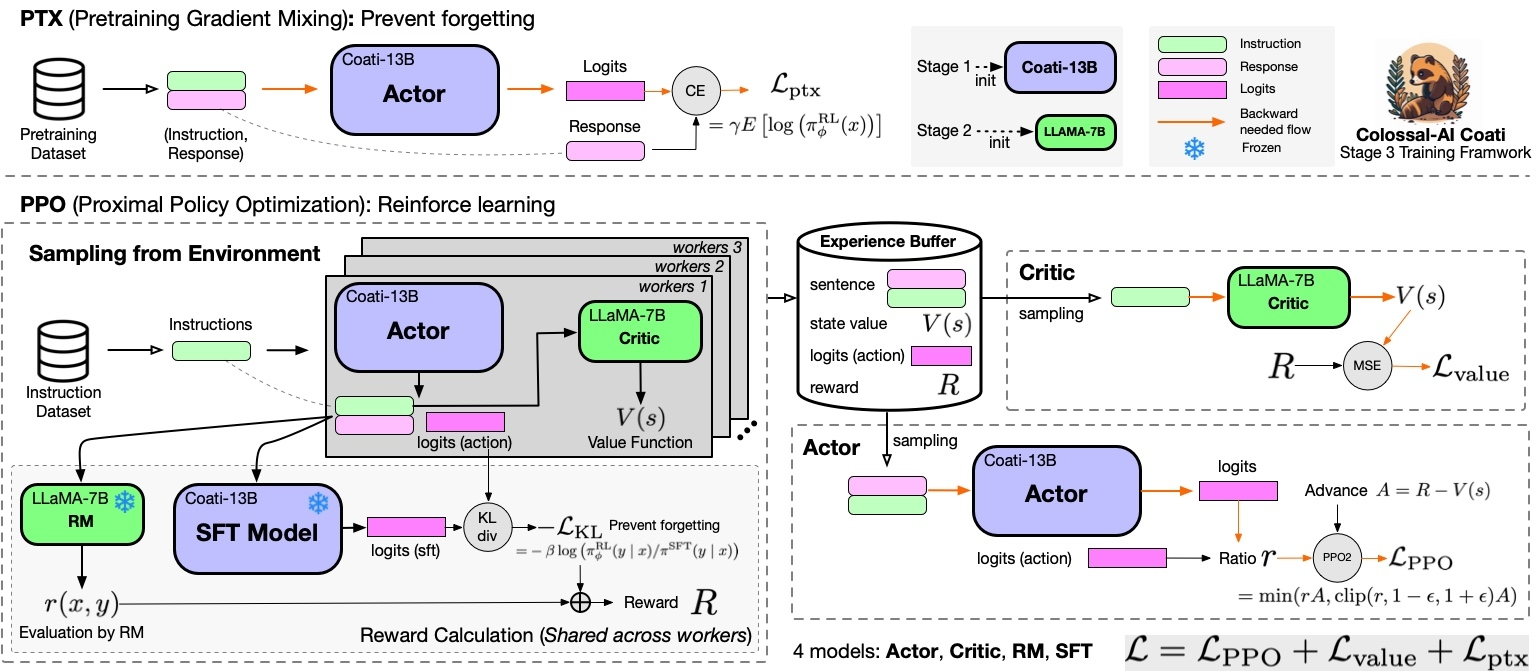
同時如果對RLHF的全流程不是特別清楚可以參照ClossalAI 的以下流程圖。非常清晰地介紹了ActorCritic這個算法是如何被運用在在InstructGPT中的RLHF流程。值得注意的是筆者與研究院的同事在訓練RLHF的時候發現要同時實現多個模型《比如actor,critic,reward model,ref model》的加載和切換比較麻煩《如果內存有限的話》。需要一些額外的工程設計《比如triton server 或者模型並行等技術》。同時不同代碼庫的實現方式和架構不同《筆者原以為部分代碼庫並沒有實現SFT模型的約束,經評論指正後筆者在三個代碼庫分別找到了對應的位置實現,都放在了Advantage計算時的代碼塊裡》
RL4LM: Is Reinforcement Learning (Not) for Natural Language Processing?: Benchmarks,Baselines,and Building Blocks for Natural Language Policy Optimization
其實近期有不少文章在探討RLHF的效率和實現方式《比如Off policy的算法做RLHF等》,其中包括如Pieter Abeel或者John Schulman的文章都非常值得一看。筆者最近在基於其中的一些想法做些實驗,如果有空也會斷斷續續總結一下,並結合自己在最近和研究院裡的小夥伴訓練RLHF的一些心得談談看法。